Программирование ветвящихся алгоритмов

    Программирование ветвящихся алгоритмов, достаточно большая тема. Рассмотрим некоторые типы задач на ветвление.
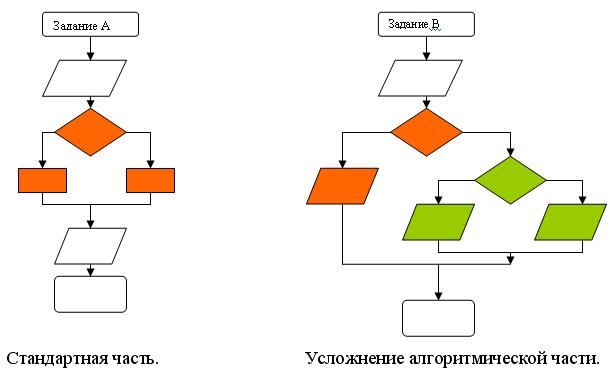
К группе А отнесем задачи где стоит выбор, какой вид ветвления использовать полную или неполную форму. 

Задание А. Дано целое число. Если оно является положительным, прибавить к нему 1, в противном случае увеличить его в два раза. Вывести полученный результат на экран.
Program n1;
Uses Crt;
Var x: Integer;
Begin
          ClrScr;
    Write('ВВеди целое число '); ReadLn(x);
    If (x>0) Then x:=x+1 Else x:=2*x;
    Writeln('x= ',x:5);
End.
    В таких задачах оператор ветвления, как правило, один. Исходные данные вводятся с клавиатуры и эти же исходные данные участвуют в условии, то есть ничего дополнительно вычислять не нужно.  
    Для усложнения могут добавляться задачи, в которых используется вложение двух или нескольких условных операторов. Хотя подобную задачу можно зачастую решить и без использования вложенных операторов ветвления.
    Задание В. Даны два числа, определить равны они или нет, если числа не равны вывести соответствующее сообщение в виде 5>2 или 2<5.
Program n2;
Uses Crt;
Var a,b:real;
begin
 write('ВВеди а = ');readln(a);
 write('ВВеди в = ');readln(b);
 if (a=b) then writeln(a:4:1,' = ',b:4:1)
          else if (a<b) then writeln (a:4:1,' < ',b:4:1)
                        else writeln (a:4:1,' > ',b:4:1);
end.
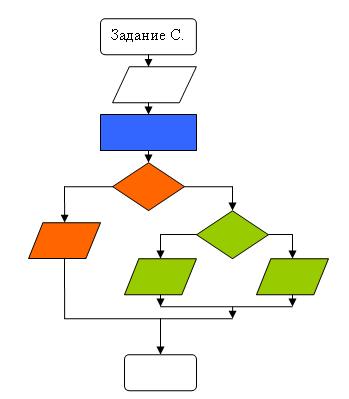
К группе С отнесем задачи где перед расчетом необходимо произвести вычисления и эти величины уже сравнивать или произвести несколько вычислений после того как проверка произведена. 
Задание С. С клавиатуры вводятся координаты двух точек на плоскости. Составить программу, определяющую, какая точка лежит ближе к началу координат.
Program n3;
Uses Crt;
Var x1,y1,x2,y2,a,b:real;
begin
   ClrScr;
   write('ВВеди X1 = ');readln(x1);
   write('ВВеди Y1 = ');readln(y1);
   write('ВВеди X2 = ');readln(x2);
   write('ВВеди y2 = ');readln(y2);
   a:=sqrt(sqr(x2)+sqr(y2));
   b:=sqrt(sqr(x1)+sqr(y1));
   if (a=b) then writeln('Расстояния равны ')
          else if (a<b) then writeln ('Вторая точка ближе')
                              else writeln ('Первая точка ближе');
end.
Сначала вычисляются расстояния от начала координат до точек, а потом эти расстояния сравниваются.
Уровень усложнения задач можно хорошо увидеть на блок-схемах.    
 

 
Усложнение  математического аппарата.

Особый интерес представляют задачи на программирование ветвящихся алгоритмов так или иначе связанные с математикой. Здесь усложнение может идти за счет большего погружения в математику. В этой группе можно рассмотреть задачи на классификацию геометрических объектов треугольников, трапеций, четырехугольников, если заданы разные элементы этих фигур.
Задание  В.     Даны три числа являющиеся углами треугольника. Классифицировать этот треугольник (равносторонний, равнобедренный, прямоугольный, разносторонний, остроугольный, тупоугольный)
Program n4;
Uses Crt;
Var a,b,c: Integer;
Begin
 ClrScr;
 Write('ВВеди A'); ReadLn(A);
 Write('ВВеди B'); ReadLn(B);
 Write('ВВеди C'); ReadLn(C);
 If (a=b) and (b=c) then Writeln ('Равносторонний');
 If (a=b) or (b=c) or (a=c) then Writeln ('Равнобедренный');
 If (a=90) or (b=90) or (c=90) then Writeln ('Прямоугольный');
 If (a<>b) and (a<>c) and (b<>c)then Writeln ('Разносторонний');
 If (a<90) And (b<90) And (c<90) then Writeln ('Остроугольный');
 If (a>90) or (b>90) or (c>90) then Writeln ('Тупоугольный');
End.
Если немного изменить задачу, то ее можно отнести к категории задач С.  
    Задание С. Даны три натуральных числа. Определить могут ли они являться углами треугольника. Если могут, то классифицировать этот треугольник (равносторонний, равнобедренный, прямоугольный, разносторонний, остроугольный, тупоугольный).
Program n5;
Uses Crt;
Var a,b,c: Integer;
Begin
 ClrScr;
 Write('ВВеди A'); ReadLn(A);
 Write('ВВеди B'); ReadLn(B);
 Write('ВВеди C'); ReadLn(C);
 if (a+b+c=180) then begin
   If (a=b) and (b=c) then Writeln ('Равносторонний');
   If (a=b) or (b=c) or (a=c) then Writeln ('Равнобедренный');
   If (a=90) or (b=90) or (c=90) then Writeln ('Прямоугольный');
   If (a<>b) and (a<>c) and (b<>c)then Writeln ('Разносторонний');
   If (a<90) And (b<90) And (c<90) then Writeln ('Остроугольный');
   If (a>90) or (b>90) or (c>90) then Writeln ('Тупоугольный');
   end
  else writeln('Это не углы треугольника ');
End.
    Здесь будет использоваться конструкция вложенное ветвление. Первое ветвление определяет могут ли числа являться углами треугольника, а в одну из ветвей этого ветвления необходимо вставить условия классифицирующую треугольники. Естественно, что необходимо вспомнить, что сумма углов треугольника равна 180 градусам.