Программирование циклических алгоритмов
В теме программирование циклов можно выделить несколько разделов. Я рассмотрю три, на мой взгляд, основных раздела. На основе изучения, которых формируется понятие циклического алгоритма. К этим разделам относятся:
1. Создание геометрических орнаментов при помощи циклов.
2. Построение таблицы значений функции на интервале.
3. Вычисление суммы (произведения) нескольких слагаемых (множителей).
Для изучения данной темы скачайте презентацию "Программирование циклических алгоритмов" с "Учительского портала" http://www.uchportal.ru/load/18-1-0-25427
Создание геометрических орнаментов при помощи циклов
Рассмотрим задачи, относящиеся к группе геометрических орнаментов. На подобных задачах проще всего объяснить понятие цикла, виды цикла и вложенные циклы. К задачам группы А, я отношу те задачи, в которых изменяется только одна переменная. При их решении можно использовать любой из трех видов циклов. Хотя чаще всего я предлагаю решить эту задачу, используя все три вида циклов. Это позволяет лучше понять, как работает тот или иной цикл и изучить его особенности.
При решении данной задачи требуется определить, какая переменная будет изменяться, какое начальное значение будет у этой переменной, какое конечное, с каким шагом будет происходить изменение.
Задание А. Построить геометрический орнамент.

Program n1;
Uses Crt, GraphABC;
var x,i:Integer;
begin
x:=1;
For i:=1 to 64 do begin
line(320,400,x,1);
x:=x+10;
end;
end.
К группе B я отношу задачи, в которых изменяются две переменные. В этих задачах усложнение зависит от того, сколько переменных будет изменяться, и с каким шагом будут изменяться переменные, так как экран имеет форму прямоугольника. В следующей задаче внутри одного цикла происходит изменение двух переменных X и Y.
Задание В. Построить геометрический орнамент.

Program n2;
Uses Crt, GraphABC;
var x,y:Integer;
begin
x:=1;
y:=1;
repeat
Line (x, 0 , 0 , y);
x:=x + 16;
y:=y + 10;
until (x>640);
end.
К заданиям С, я отношу задачи в которых при создании орнамента используются вложенные циклы. В этих задачах необходимо так построить алгоритм, что бы внутри одного цикла находился другой цикл. Усложняя задачу, можно предложить орнамент, в котором количество элементов в каждом ряду неодинаково. Такие задачи позволят в дальнейшем легче перейти к программированию двумерных массивов.
Задание С. Построить геометрический орнамент.

Program n3;
Uses Crt, GraphABC;
var x,y:Integer;
begin
y:=10;
while (y<350) do begin
x:=10;
y:=y + 25;
while (x<620) do begin
circle(x,y,10);
x:=x+25;
end;
end;
end.
Построение значений функции на интервале
Алгоритм решения данных задач достаточно простой, поэтому усложнение заданий идет в сторону математики.
Для задач группы А, предлагается построить таблицу непрерывной на данном интервале функции. В этом случае используется только оператор цикла, чаще всего Repit Until. Цикл For to do в Паскале не совсем подходит, так как в нем отсутствует параметр шаг, а точное количество итераций часто подсчитать достаточно сложно.
Задание А.Построить таблицу значений функции y = 3 sin x + cos 2x на интервале [ -Pi/6 ; Pi/6] с шагом Δх = 0,1.
Program n4;
Uses Crt;
var x,y,dx:real;
begin
ClrScr;
x:=-Pi/6;
dx:=0.1;
writeln (' x y');
repeat
y:= 3* sin(x) + cos(2*x);
writeln (x:10:5,y:10:5);
x:=x+dx;
until (x>pi/6);
end.
В группе задач В подбираются такие функции, что бы они имели разрыв на области определения. Это может быть тангенс, котангенс или дробь. Здесь требуется добавить условие, которое не даст вычислять значение функции в определенных точках. Дополнительная сложность здесь появляется в выражении функций, которых нет в стандартном наборе языка Pascal.
Задание В. Построить таблицу значений функции y = сtg x, на интервале [-1 ; 1] с шагом Δх = 0,1.
Program n5;
Uses Crt;
var x,y,dx:real;
begin
ClrScr;
x:=-1;
dx:=0.1;
writeln (' x y');
repeat
if (x<>0) then begin
y:= cos(x)/sin(x);
writeln (x:10:5,y:10:5);
end;
x:=x+dx;
until (x>=1);
end.
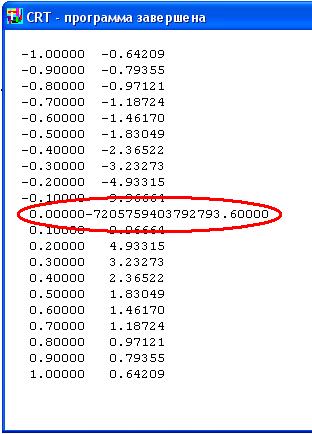
В том месте, где должен быть пропущен 0, стоит какое то странное число. Это связано с особенностью работы системы программирования PascalABC с десятичными дробями. Поэтому внесем в программу такие изменения, если число по модулю меньше 0.000000000001 будем считать что это 0.
Program n5;
Uses Crt;
var x,y,dx:real;
begin
ClrScr;
x:= -1;
dx:=0.1;
repeat
if (abs(x)>1e-12) then begin
y:= cos(x)/sin(x);
writeln ('x= ',x:10:5,' y= ',y:10:5);
end;
x:=x+dx;
until (x>=1);
end.
Наиболее сложно задание - построить таблицу значений функции заданной кусочно. Здесь требуется внутри цикла организовать вычисление значений различных функций на трех или более интервалах.
Для тех кто забыл что это такое, рекомендую посмотреть № 46, 51, 55 учебника «Алгебра и начала анализа 10-11 класс» (Под редакцией А.Н. Колмогорова). В этих номерах приводятся примеры таких функций и их графиков.
Задание С. Построить таблицу значений функции на интервале [-2; 2] с шагом Δх = 0,1 если функция имеет вид
x+1, при x<-1
Y= x2 , при -1<=x<=1
x -2, при x>1
Program n6;
Uses Crt;
var x,y,dx:real;
begin
ClrScr;
x:=-2;
dx:=0.1;
writeln (' x y');
repeat
if (x<-1) then y:=x+1;
if (x>=-1) and (x<=1) then y:=x*x;
if (x>1) then y:=x-2;
writeln (x:10:5,y:10:5);
x:=x+dx;
until (x>=2+dx);
end.
В этой задаче в цикл добавляется три условия, в зависимости от которых вычисляется одна из трех функций. В одном из условий нужно правильно указать интервал, используя связку And, так как двойные неравенства в условии использовать нельзя. Все это требует от программиста более глубоких познаний в математике.
Вычисление суммы (произведения) нескольких слагаемых (множителей)
Вычисление суммы или произведения, наверное, самая большая по количеству и качеству задач. Здесь рассматриваются задачи на нахождение суммы конечного и бесконечного ряда, задачи эксперименты в которых высчитывается сумма того, что заранее неизвестно, нахождение площади фигуры ограниченной кривой линией и т.д. В этой работе я покажу, как меняется сложность задач на примере нахождения суммы конечного ряда и нахождение площади криволинейной трапеции.
Самые простые задачи в которых меняется параметры в цикле. Как правило подобные задачи очень похожи друг на друга.
Задание А. Даны два целых числа А и В (А < В). Найти сумму всех целых чисел от А до В включительно.
Program n7;
Uses Crt;
var s,a,b,i:integer;
begin
ClrScr;
s:=0;
write('Введи а= ');Readln (a);
write('Введи b= ');Readln (b);
for i:=a to b do s:=s + i;
writeln('s= ',s:5);
end.
В этой задаче все четыре переменные могут быть целого типа. Требуется ввести необходимые значения с клавиатуры и правильно организовать цикл.
Задание В. Дано целое число N (N>0). Используя один цикл найти сумму S=1+1/2!+1/3!+...+1/N!.
Program n8;
Uses Crt;
var s,f:real;
i,n:integer;
begin
ClrScr;
write('ВВеди N= ');readln(n);
s:=1;f:=1;
for i:= 2 to n do begin
f:=f*i;
s:=s+1/f;
end;
writeln('Сумма = ',s:10:9);
end.
В этой задаче в одном цикле приходится объединять нахождение суммы и вычисление факториала очередного слагаемого. Кроме того, необходимо помнить, что в операторе For To Do переменные i и n должны быть целого типа, а сумма будет выражаться десятичной дробью. Это должно быть отражено в разделе описания переменных.
В задания С хорошо рассматривать на задачах нахождение площади криволинейной трапеции. Если к этому моменту вы не знакомы с интегрированием, советую посмотреть хотя бы в интернете геометрическую интерпретацию интеграла. Идея разбиения криволинейной трапеции на отдельные полоски прямоугольной формы достаточно проста.
Задание С. Вычислить площадь фигуры ограниченной линиями: X=1, X=4, Y=0, Y=1/X .
Program n9;
Uses Crt;
Var x,h,s:Real;
Begin
ClrScr;
h:=(4-1)/1000;
x:=1;
Repeat
s:=s+h*1/x;
x:=x+h;
Until x>4;
writeln('Площадь = ',S:10:5);
end.
В этой задаче уже нельзя использовать цикл с параметром. Нужно сначала определить шаг (ширину полоски) а затем в операторе цикла с постусловием находить сумму площадей этих полосок.



